What is Basic Reproduction Number R0 (R naught)
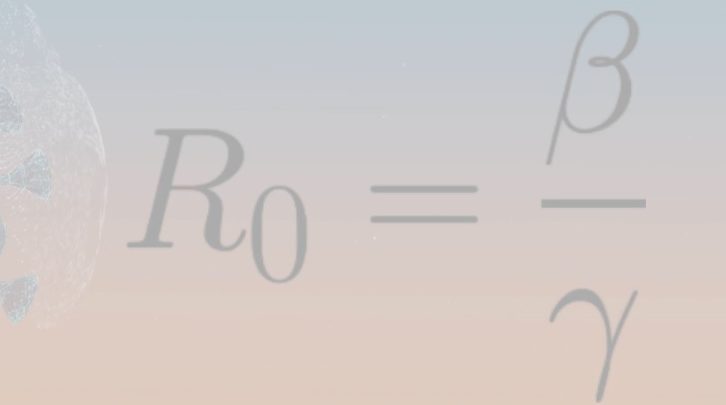
The infectivity of a pathogen can be estimated by mathematical models that calculate the basic reproduction number (R0, R naught), defined as the number of secondary infections expected from each case of a disease in a fully susceptible population. Table 1 shows the value of R0 for selected infectious diseases.
[table id=2 /]
Table 1: Basic reproduction number R0 and community immunity needed to protect society from certain infectious diseases. (1)R0 and community immunity values are the highest estimates for each disease. Community immunity values have only been shown for diseases in which the vaccine is available. (2) The values shown are for pandemic (H1N1) 2009 flu. Each flu epidemic has a different R0 and community immunity value. Society agrees that immunity is a 100% effective vaccine. Vaccine effectiveness in flu is 6o% and observed community bond values are 40% or greater depending on susceptible host populations.
The value R0 estimates the risk of disease spread in a population. Having a R0 value of 1 means that each infected person will infect a susceptible person and the disease will last in the population. The fact that R0 is greater than 1 means that each infected person will spread the epidemic by passing the disease to more than one susceptible person, leading to a possible epidemic and even pandemic. On the contrary, a R0 smaller than 1 indicates that each infected person will pass the disease to one less susceptible person and that the disease will disappear under these conditions.
R0 is directly linked to the community immunity needed to prevent the spread of infection; as the value of R0 rises, a larger community immunity is needed to stop infection. For example, under ideal conditions, 94% of the population (R0 = 18) must be immune to stop the spread of the highly infectious measles virus, while only 29% of the population (R0 = 1,6) must be immune to stop the spread of the flu (see table 1). Unfortunately conditions are not always ideal, and mathematical models estimating R0 may not take into account factors such as the number of people recovering, population density (close contact), length of contact time, and other variables that may affect disease spread. Ultimately R0 can only predict theoretical infectivity but is still useful as a comparative measure of the relative infectivity of a pathogen and helps determine immunisation coverage targets to prevent disease spread.
The observed reproductive number calculated from actual disease spread studies, R, is a more useful term because it takes into account the actual transmission observed from infected individuals to susceptible individuals. For most disease outbreaks, R cannot be realistically obtained because precise information about disease spread is not available; too many individuals have been implicated to accurately track the source of each infection. However, R 3.6 was observed in the 2003 SARS outbreak. Public health officials recognize the potential for a serious epidemic and have instituted infection controls such as isolation of infected people and strict barrier protection for medical personnel. These measures reduced the SARS R value to 0.7, ending the danger of further spread of the disease. Likewise in an Ebola filovirus outbreak (see table 1) the number of reproduction was reduced from a theoretical 1.8 R0 to 0.7 R, again using strict infection control measures that prevent the spread of infection and thus eliminate a potential epidemic and pandemic.



